Significant Discrepancy in SiC MOSFET Loss Calculation: Custom Script vs PLECS Lookup Table (C3M0021120K / C3M0015065K)

General
, ,
1

Hello,

I’m developing a custom power loss calculation script for rapid topology evaluation under varying load conditions. To validate its accuracy, I compared its results against PLECS thermal simulations based on a T-type three-level inverter using discrete SiC MOSFETs (C3M0021120K and C3M0015065K ). Despite both methods using identical voltage/current waveforms, I observe significant discrepancies between my script and PLECS(Psw=13.72 per phase for PLECS and Psw=10.50 per phase for script). I suspect differences in lookup table implementation are the root cause and seek clarification.

My script computes switching losses by first determining losses at measured current, then scaling for voltage, junction temperature, and gate resistance based on datasheet curves and typical reference conditions. Given that PLECS appears to use limited lookup table data, I suspect differences arise from its interpolation methodology: Could you clarify whether PLECS employs piecewise linear interpolation or polynomial fitting between table points? Additionally, I’d appreciate insights into how PLECS handles multi-variable dependencies (e.g., simultaneous Esw = f(Ids, Vds, Tj, Rg)) and extrapolation beyond datasheet ranges. As both approaches use identical operational parameters, understanding PLECS’ underlying algorithm would help resolve this inconsistency.

Best regards,
Yuhao Wang

2

Dear Yuhao,

Thank you for your detailed description. From what you’ve explained, it seems that your approach differs from how PLECS handles switching losses. You appear to be using a stepwise method — starting with losses at the measured current and then applying scaling for voltage, junction temperature, and gate resistance. In contrast, PLECS performs this calculation in a single step using predefined lookup tables. Given this fundamental difference, it’s not surprising that the results may diverge.

Could I ask where you’re sourcing your data from for the loss curves and scaling factors?

Regarding your question on interpolation: PLECS uses linear interpolation within the lookup table, as this is the most appropriate method without detailed knowledge of the device physics. If the input falls outside the provided data range, PLECS applies linear extrapolation.

I’d also recommend taking a look at the tutorial PLECS: Thermal Simulation of a Buck-Converter. Since it involves only a single MOSFET, it’s a more controlled setup and can serve as a helpful reference for comparing your script and pinpointing potential sources of discrepancy.

Best regards,
Reto

3

Dear Reto,

Thank you for your explanation.

I now better understand the potential causes for the divergence in results. To clarify PLECS’ underlying process: Could you elaborate on how PLECS computes switching losses in a single interpolation step across multiple variables? The switching losses are related to the measured current, voltage, junction temperature. For instance, the predefined lookup tables include 8 data point about switching energy at Ids=10A/20A, Vds=600V/800V, Tj=75°C/125°C. How does PLECS derive the value at intermediate conditions like Ids=15A, Vds=400V, Tj=100°C? If PLECS uses linear interpolation, it seems that the script results should nearly match a stepwise approach.

All data originates from Wolfspeed’s datasheets. In my script, I fitted curves for switching energy versus current, junction temperature, and gate resistance independently. For voltage scaling, I calculated a proportional factor at 400V by comparing the datasheet’s switching energy values at 800V/50A versus 600V/50A.

I’ve attached my fitted turn-on switching energy curve for reference.

Best regards,
Yuhao Wang

4

C3M0021120K_Eon&Ids
C3M0021120K_Eon&Ids1087×548 29.7 KB

5

Dear Yuhao,

First, regarding the screenshot you sent:

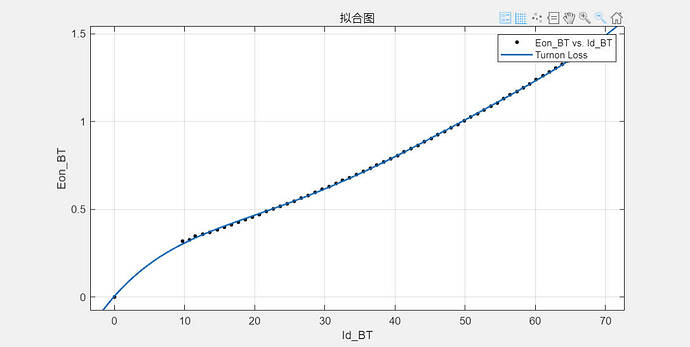
If this represents turn-on data at 800 V and 25 °C, and the y-axis is in mJ, then it appears to be quite similar. However, it seems you’re working with a different dataset than the one used in PLECS. As a result, the total losses differ, which makes it impossible to pinpoint the exact source of the discrepancy. For this reason, it’s crucial to always begin with the same data set to ensure a meaningful comparison.

Additionally, your fitting function seems to generate values between 0 and 10 A that are not present in the original data—at least based on what has been provided. This could introduce misleading artifacts and should be addressed.

PLECS uses 3D lookup tables for modeling turn-on and turn-off losses. The loss energy is computed as a function of current, voltage, and temperature:
Eon = f(v, i, T).
All interpolation is performed directly within these 3D lookup tables.

I’ve attached a test model that can be used to evaluate the switching and conduction losses within PLECS. In the relevant subsystem, you can define the thermal description, which internally passes the data to the 3D and 2D lookup tables (you can press Ctrl+U to look beneath the mask). The block takes current, voltage, and temperature as inputs, and outputs the switching and conduction losses.

Note: This block is intended for validation purposes only and should not be used in
simulations.

thermal_validation.plecs (18.6 KB)
C3M0120090D_tutorial.xml (2.9 KB)

Suggested Workflow:

To ensure consistent and meaningful comparisons between your script and PLECS, I recommend the following steps:

  1. Start with a simple model
    Use a minimal example that includes only one switching device. I used the buck converter from the tutorial referenced earlier for this purpose.
  2. Use identical input data
    Ensure that both PLECS and your script use the same current, voltage, and temperature values.
  3. Start with a known reference point
    Perform loss calculations for a defined operating point (e.g., 400 V, 15 A, , 25 °C) to establish a baseline.
  4. Verify 1D interpolation
    Change only one parameter (e.g., vary the current to 10 A while keeping voltage and temperature fixed at 400 V, 25 °C). This simplifies validation and makes it easier to manually assess interpolation behavior.
  5. Repeat step 4 for other parameters
    Individually sweep voltage or temperature while holding the others constant.
  6. Test 2D interpolation
    Fix one parameter and sweep the remaining two. This allows you to assess two-dimensional interpolation consistency.
  7. Test full interpolation behavior
    Choose a point where all three parameters (v, i, T) are set to values not explicitly contained in the original dataset. This helps evaluate how both models behave under full interpolation conditions.

By systematically following these steps, you should be able to pinpoint where any differences between your script and PLECS originate.

Best regards,
Reto

1 Like
6

Dear Reto,

Thank you for your valuable suggestions.

All data originate directly from Wolfspeed’s datasheets, including the limited operating points available in PLECS’ lookup tables. In your way, it seems that PLECS’ approach may provide higher accuracy.

In practice, the script’s calculation methodology follows established approaches from IEEE journals on power loss modeling. It first fits the switching loss curve against current to derive a polynomial expression, then applies linear scaling factors for voltage and junction temperature corrections. Could you clarify whether it introduces significant calculation errors specifically in the context of SiC MOSFET loss modeling?

Additionally, would it be possible to share a low version of the test model (compatible with PLECS 4.1)?

Thank you again for your expertise.

Best regards,
Yuhao Wang

7

Please find attached a version that works with PLECS 4.1—hope that helps!
thermal_validation_4_1.plecs (16.0 KB)

8

My understanding is that Wolfspeed’s thermal models are derived using in-house characterization data from bench testing, and we wouldn’t know if their data sheets are always using the exact same source data. Perhaps you can also contact them to better understand their data and models, though!