DQ Transformation
Multiple conventions exist for the DQ (direct-quadrature) transformation, differing in frame alignment and axis ordering. The choice of convention affects the resulting equations and signs in the model.
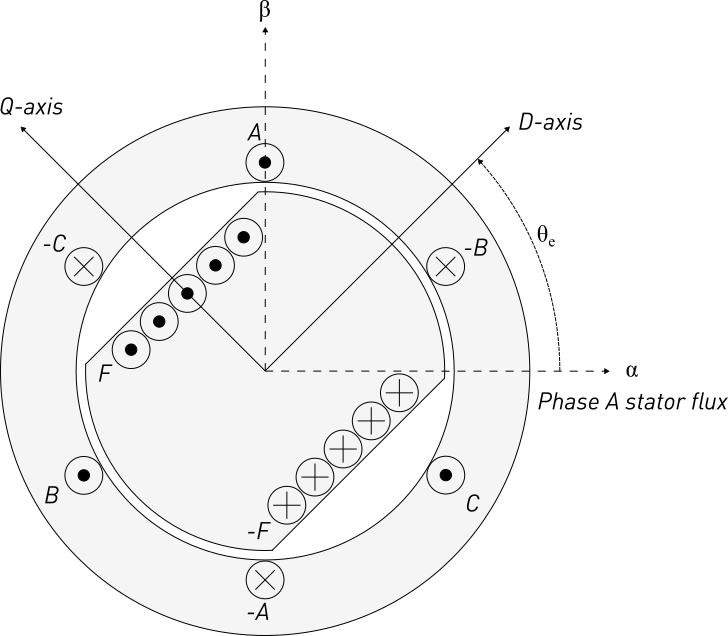
The convention used in PLECS is shown in Fig. 1 highlighting:
- The rotor’s electrical angle \theta_e is measured from the phase A flux to the rotor’s angular position.
- The D-axis is aligned with the stator’s phase A winding flux linkage when the rotor’s electrical angle \theta_e=0.
- The Q-axis leads the D-axis by 90 degrees.
- Positive Q-axis current (i_q>0) produces positive electrical torque.
- The D-axis corresponds to the magnetic north of the rotor, whether that is generated by permanent magnets or a positive field winding current.
Figure 1: Electric Machine Axis Conventions
This behavior corresponds to the formulation of the abc to stationary (\alpha\beta) and abc to rotating (DQ) transforms in the PLECS manual:
\begin{align*} \left[\!\! \begin{array}{c} y_\alpha \\ y_\beta \end{array} \!\!\right] = \left[ \begin{array}{ccc} \frac{2}{3} & -\frac{1}{3} & -\frac{1}{3} \\ 0 & \frac{1}{\sqrt{3}} & -\frac{1}{\sqrt{3}} \end{array} \right] \cdot \left[\!\! \begin{array}{ccc} x_\mathrm{a} \\ x_\mathrm{b} \\ x_\mathrm{c} \end{array} \!\!\right] \end{align*}
\begin{align*} \left[\!\! \begin{array}{c} y_\mathrm{d} \\ y_\mathrm{q} \end{array} \!\!\right] = \frac{2}{3} \left[\!\! \begin{array}{ccc} ~~~\cos \theta_{e} & ~~~ \cos \left(\theta_{e}-120^\circ\right) & ~~~ \cos \left(\theta_{e} +120^\circ\right) \\ -\sin \theta_{e} & -\sin \left(\theta_{e}-120^\circ\right) & -\sin \left(\theta_{e} +120^\circ\right) \end{array} \!\!\right]\!\!\! ~\cdot \left[\!\! \begin{array}{ccc} x_\mathrm{a} \\ x_\mathrm{b} \\ x_\mathrm{c} \end{array} \!\!\right] \end{align*}
If you implement a controller designed for a different convention, you may need to swap i_d and i_q references, negate certain terms, or adjust the angle transformation by \pm 90^\circ.
Electrical and Mechanical Quantities
The electric rotor angle \theta_e is used in the DQ transformation and appears throughout the machine equations. However, one can only directly measure the machine shaft’s mechanical quantities using the Rotational Speed Sensor and Angle Sensor (or measure these quantities using the PLECS Probe).
The mechanical quantities for speed \omega_m in rad/s and angle \theta_m in rads often need to be converted to the corresponding electrical quantities by multiplying by the number of pole-pairs p:
\begin{align*} \omega_e &= p \omega_m\\ \theta_e &= p \theta_m \end{align*}
Common mistakes include:
- Using mechanical angle and speed when electrical quantities are required.
- Use of alternative units such as degrees for angle or RPM for speed without converting to correct SI units of angular frequency in rad/s and angular position in rads.
Generator and Motor Operation
All machines in PLECS can operate in either motor or generator mode. If the mechanical torque has the same sign as the rotational speed the machine is operating in motor mode, otherwise in generator mode.
The table below summarizes the different motor and generator operating modes, using the convention that a positive torque and speed is the forward mode.
| Quadrant | Speed | Torque | Mode | Power Flow |
|---|---|---|---|---|
| I | + | + | Forward motoring | Electrical → Mechanical |
| II | + | − | Forward generating (braking) | Mechanical → Electrical |
| III | − | − | Reverse motoring | Electrical → Mechanical |
| IV | − | + | Reverse generating (braking) | Mechanical → Electrical |
Current Direction Convention
Current direction conventions determine the sign of electrical power and must be consistent throughout the model. The PLECS convention is:
- Positive current flows into the machine’s stator terminals from the external electrical network
- This matches the standard motor convention used in most electrical machinery textbooks
- Positive real power (P > 0) flows into the machine in motor mode
Understanding Back EMF Constant, Torque Constant, and Flux Linkage
The Permanent Magnet Synchronous Machine (PMSM) and Brushless DC Machine (BLDC) components in the PLECS library require users to enter a parameter characterizing the strength of magnetic flux.
Motor manufacturers use various conventions for specifying back EMF constant K_e, torque constant K_t, and permanent magnet flux \phi. The most common variations involve:
- Voltage measurement: Line-to-neutral vs. line-to-line
- Voltage amplitude: Peak vs. RMS quantities
- Speed units: Mechanical rad/s vs. mechanical RPM vs. mechanical kRPM
- Torque units: SI units such as newton meters (N-m) vs. imperial units such as ounce-inches (oz.-in) or pound-feet (lb-ft)
PLECS Conventions
In PLECS the BLDC (Simple) machine’s back EMF constant K_e is defined in units of V_{LN,pk} /\omega_m where \omega_m is in mechanical rad/s. The BLDC model uses K_e because it’s more directly related to measurable back EMF, especially when considering both trapezoidal and sinusoidal back EMF shapes.
The PMSM machines in PLECS use the flux induced by the permanent magnet \phi in units of volt-seconds (Vs) or webers (Wb). The induced flux is a logical choice as it appears in the DQ frame flux linage equations.
Note that these parameters all represent the same basic physical phenomena - the magnetic coupling of the rotor magnets and the stator.
For machines with sinusoidal back EMF the relationship between the flux linkage and back EMF constant is: K_e = p\phi where p is the number of pole-pairs.
Conversion Table for Common K_e Datasheet Formats
The table below provides the coefficients to convert between common datasheet formats for K_e and PLECS back EMF convention for the BLDC (Simple) machine model with Sinusoidal flux. The equivalent PMSM flux linkage coefficient requires accounting for the number of pole-pairs with an additional 1/p scaling factor.
| Datasheet Format | Conversion to PLECS Ke | Notes |
|---|---|---|
| Vln,peak / (rad/s) | 1 | Direct match - no conversion needed |
| Vll,peak / (rad/s) | 1/{\sqrt{3}} | Convert line-to-line to line-to-neutral |
| Vln,RMS / (rad/s) | \sqrt{2} | Peak is \sqrt{2} RMS for sinusoidal waveforms |
| Vll,RMS / (rad/s) | \sqrt{2/3} | Combine both conversions |
| Vln,peak / RPM | \frac{60}{2\pi} | Convert RPM to rad/s |
| Vll,peak / kRPM | \frac{60}{2\pi}\frac{1}{1000}\frac{1}{\sqrt{3}} | Most common industrial format |
| Vll,RMS / kRPM | \frac{60}{2\pi}\frac{1}{1000}\sqrt{\frac{2}{3}} | Combines RMS, line-to-line, and kRPM |
The attached model shows the conversion from Vll,peak/kRPM to equivalent parameters for the PMSM and BLDC machine models, and compares the open winding line-to-line voltages at 1 kRPM to the specified constant. Note that the peak line-to-neutral voltage induced by the back EMF is K_e\omega_m.
Ke_conversion_example.plecs (14.4 KB)
Torque Constant
Some datasheets provide a torque constant K_t relating the machine phase currents to the generated peak torque. When using the SI-based convention in PLECS K_t in N-m/A,pk is equivalent to K_e in Vln,pk-s/(rad/s).
Torque constants are sometimes specified in imperial units such as oz-in/A or lb-ft/A which are converted using standard force and length conversion factors: 1 N-m/A ≈ 141.612 oz-in/A ≈ 0.73756 lb-ft/A. Care should be taken to confirm if the datasheet currents are RMS or peak values.
Induction (Asynchronous) Machine Conventions
The induction machines in the PLECS library use a stationary reference frame (\alpha\beta) based implementation. This contrasts with synchronous machines in the PLECS library which use the rotating reference frame (DQ). This choice reflects the natural characteristics of induction machines, where there is no fixed rotor reference frame as the rotor field can rotate relative to the rotor position.
The convention used in PLECS for asynchronous machines is:
- The \alpha-axis is aligned with stator’s phase A winding flux linkage
- The \beta-axis leads the \alpha-axis by 90 degrees
- This is a stationary frame fixed to the stator, not rotating with the rotor